Georg Bergner

Lattice gauge theory

My main current investigations are related to lattice gauge theory and, more general, quantum field theory on the lattice. I am using numerical computations to study properties of quantum field theories such as particle masses and phase transitions. The approach is based on a representation of the theory on a space-time lattice. Monte-Carlo simulations provide an insight into the nonperturbative sector of the quantum field theory. Especially gauge theories with dynamical fermions like QCD and supersymmetric Yang-Mills theory in four dimensions are complex systems. They require large scale computer resources. Therefore, I am doing the computations and code development on large scale computing facilities such as provided by the Jülich Supercomputing Centre.

QCD at finite temperature and density and the lattice

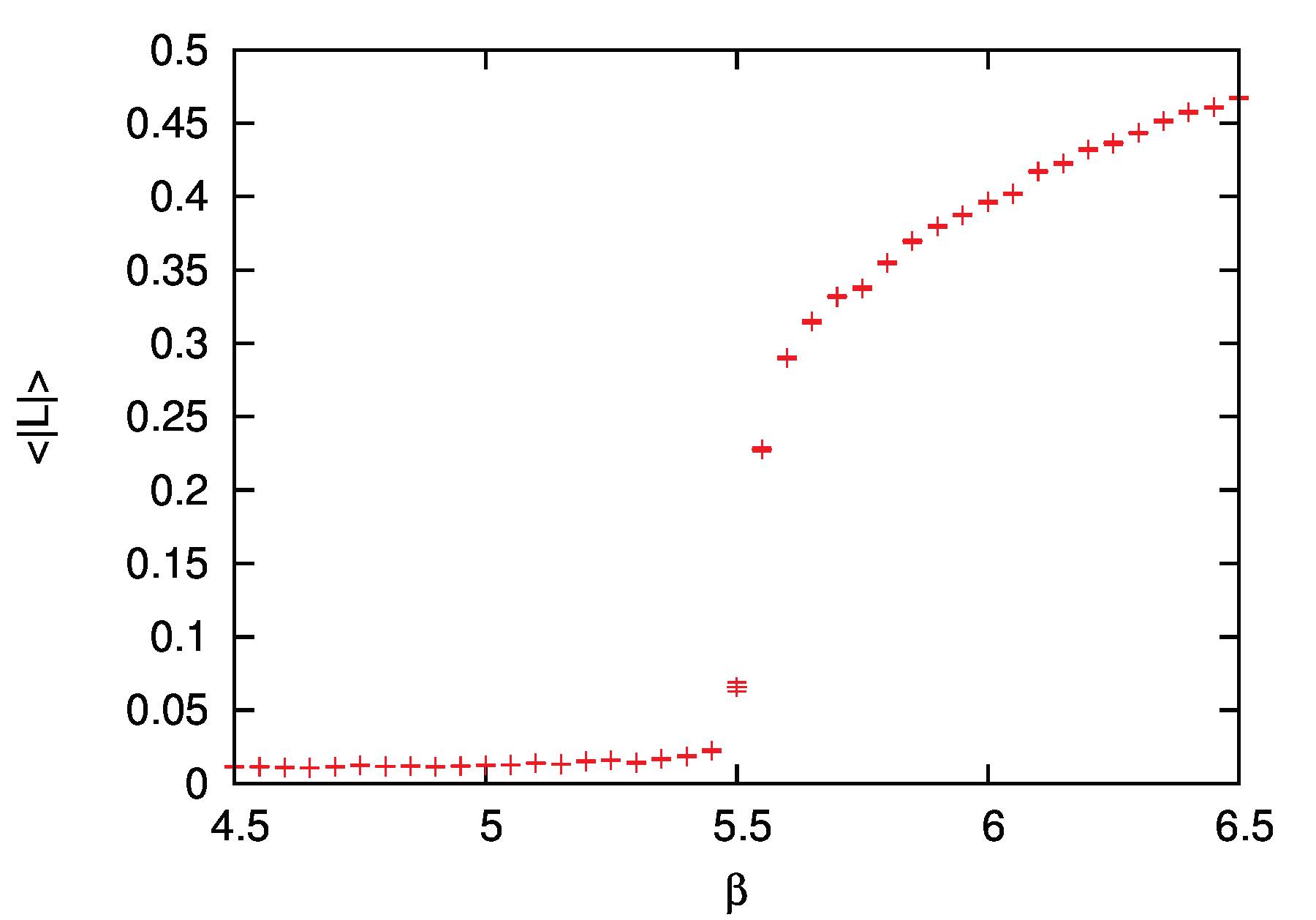
Investigations of quantum chromodynamics (QCD) at finite temperature and finite density are a challenging topic of my investigations. Lattice computations provide a successful approach to investigate strongly interacting theories like QCD. Unfortunately a severe sign problem prohibits an application of this approach at finite density. I am investigating effective models that can be derived from a strong coupling expansion of lattice QCD. These models help to find predictions for QCD at finite density. They provide also a playground for methods to understand and attack the sign problem.

Lattice simulations of physics beyond the Standard Model

The Standard Model is a well established theory describing all known elementary particles and their interactions. Despite its success, it fails to explain the large amount of dark matter found in astronomical observations. In addition, it leads to theoretical issues like the Hierarchy Problem. For these reasons, there has been a long time search for the extension of the Standard Model. Several theoretical attempts for such an extension rely on certain non-perturbative properties of strongly interacting gauge theories. The relevance of these extensions can hence only be clarified by numerical lattice simulations.
A second important goal of modern particle physics is a better understanding of the contents of the Standard Model. Several aspects of it can be analyzed based on a perturbative expansion, but the main characteristic phenomena of the strong interactions like confinement of charges, are not accessible with these methods. Investigations of non-standard version of these interactions, i.e. strongly interacting theories beyond the ones realized in the Standard Model, provide a new perspective for an analytical understanding. Interesting candidates are in particular supersymmetric versions, which, due to the enhanced symmetry, are accessible to alternative analytic approaches. These findings must be verified, generalized and extended by numerical simulations.

Supersymmetry on the lattice

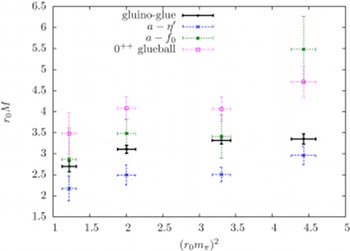
Possible extensions of the standard model of quantum field theory have been a major topic of my research and I am still interested and involved in these investigations. I started with models similar to the matter sector of supersymmetric extensions of the standard model (Wess-Zumino models). Later on I began to consider the correpsonding gauge sector (supersymmetric Yang-Mills theory) as well. Supersymmetry requires the simulation of dynamical fermions on the lattice. Therefore the simulations are similar to QCD on the lattice (with one quark flavour). Unbroken supersymmetry predicts a degeneracy of the fermionic and bosonic energy states. Consequently, each bosonic particle should have a fermionic partner with the same mass. In principle, the mass degeneracy should be obtained also in the numerical lattice simulations. However, the lattice breaks supersymmetry. More precisely, I was able to establish a No-Go theorem stating that either supersymmetry or locality must be broken in a lattice theory. The re-establishment of supersymmetry in the continuum limit of the lattice theory is the main goal of my lattice simulations. Therefore, I am studying the masses of the particles in supersymmetric Yang-Mills theory.

Gauge/Gravity Dualiy and investigations of black holes and M-theory on the lattice

The Gauge/Gravity Duality connects strongly interacting gauge theory to the theory of quantum gravity. They have been established for supersymmetric versions of the gauge theories. In particular, low dimensional supersymmetric gauge theories are an interesting playground for these dualitites. These theories are low dimensional counterparts of theories with extended supersymmetry in four dimensions. They are investigated in the large N limit, which leads to a non-trivial dynamics of the large gauge matrices. My investigations of these theories based on numerical lattice simulations provide access to the nonperturbative dynamics of these theories.

Numerical techniques of lattice gauge theory

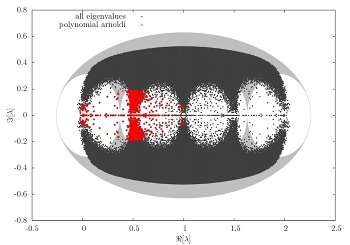
The simulation supersymmetric Yang-Mills and lattice QCD requires advanced numerical methods. Considerations and extensions of these methods are therefore an essential part for my studies. In that context I have studied methods for the calculation of the lowest real eigenmodes of large sparse matrices (the Dirac-Wilson operator). These are needed, for example, to obtain the Pfaffian sign in supersymmetric Yang-Mills theory. The measurement of the observables in supersymmetric Yang-Mills theory is also a challenging task. It requires advanced techniques for the glueball operators and meson operators with disconnected contributions.

Twisted Mass lattice QCD simulations

The long time goal of the Extended Twisted Mass Collaboration (ETMC) is to provide numerical data for a variety of QCD observables from numerical lattice simulations of the underlying quantum field theory. These data are an important input for a comparison with the experimental data and the search for new bound states and QCD effects. The precision of the numerical data is currently substantially increasing and even challenging large scale simulations at physical pion masses become available. I have joined the effort of the ETMC in obtaining a more precise and complete view of QCD properties.

Lattice representations of symmetries

I am investigating if a similar solution as for the chiral symmetry on the lattice can be found for supersymmetry. Like supersymmetry, the chiral symmetry can not be represented on the lattice in a straight forward way. The solution is a renormalization group step that maps the continuum theory onto the lattice. The symmetry is expressed in terms of a relation on the lattice (Ginsparg-Wilson relation). I have generalized this approach for an arbitrary symmetry (including supersymmetry).

Functional renormalization group flow

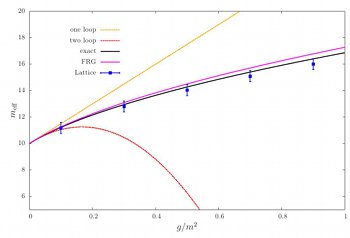
Since there is no straight forward implementation of supersymmetry on the lattice it is helpful to compare the results with other methods. The functional renormalization group flow offers an interesting non-perturbative method as alternative for the lattice simulation. Therefore a comparison of these methods is one of my current research interests.