Quantum field theory 2, lecture 16

Action for lattice gauge theory

Adding them and expanding the exponentials gives \[\begin{split} W_{\text{plaq}}+W_{\overline{\text{plaq}}} = 2N -a^4 \text{Tr}\left\{\mathbf{F}_{12} \mathbf{F}^{12}\right\} + \ldots \end{split}\] Interestingly, this is precisely of the form we need for the action. We can take the lattice action of Yang-Mills theory to be \[\begin{split} S[U] = - \frac{1}{2g^2} \sum_{\text{plaq}} W_{\text{plaq}}, \end{split}\] where the sum goes over the plaquettes around each lattice point including both orientations. Each plaquette is expressed as the product of four link matrices \(U\).

Functional integral

The functional integral can be written as an integral over these link matrices, \[\begin{split} Z = \int \mathcal{D}U ~e^{-S[U]}, \end{split}\] where \[\begin{split} \mathcal{D}U = \prod_{\text{links}} dU_\text{links}, \end{split}\] and \(dU\) is the Haar measure associated with the group \(\text{SU}(N)\). It has the properties (for \(N\ge 3\)) \[\begin{split} &\int dU~U_{ij} = 0,\\ &\int dU~U_{ij}U_{kl} = 0,\\ &\int dU~U_{ij}U_{kl}^* = \frac{1}{N}\delta_{ik}\delta_{jl}. \end{split}\]

Wegner-Wilson loop at strong coupling

Let us now consider a Wilson loop composed of a sequence of link variables, \[\begin{split} \langle W_{\mathcal{C}}\rangle = \frac{1}{Z} \int \mathcal{D}U \, W_{\mathcal{C}} \, e^{-S[U]}. \end{split}\] We will evaluate this in the strong coupling expansion in powers of \(1/g^2\). To lowest order, \(e^{-S[U]}\to 1\) and the result vanishes because \(\int dU~U_{ij}=0\) for each link. Clearly, each link \(U\) in \(W_{\mathcal{C}}\) must be balanced by a conjugate link \(U^*\) from the expansion of \(e^{-S}\).

To get a non-zero result, we must fill the interior of the Wilson loop by opposite plaquettes from the action using a division like the following.

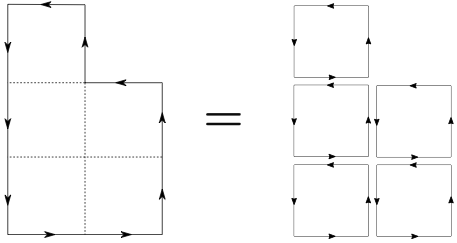
Each plaquette comes with a factor \(1/g^2\) and the number of plaquettes needed is the area \(A/a^2\). Accordingly, \[\begin{split} \langle W_{\mathcal{C}}\rangle = \text{const} \times \left[\frac{1}{g^2}\right]^{A/a^2} = \text{const} \times e^{-\sigma A}, \end{split}\] where \[\sigma = \frac{\ln(g^2)}{a^2},\] is the string tension.

Area law and confinement

This area law is a signal for confinement. The consideration of a static quark-antiquark pair now leads to \[\langle W_{\mathcal{C}}\rangle = \text{const} \times e^{-\sigma R T},\] and thus the potential between static charges in linear, \[\begin{split} V(R) = \sigma R. \end{split}\] The energy becomes infinitely large when one tries to separate the quark and anti-quark. In reality, the string breaks when the energy is large enough to produce another quark-antiquark pair.

Implementing lattice QCD numerically, one can go beyond the strong and weak coupling expansions.

The standard model

Gauge group of the standard model

The gauge group of the standard model of elementary particle physics is \[\text{SU}(3) \otimes \text{SU}(2) \otimes \text{U}(1).\] The fermion fields and the Higgs boson scalar field can be classified into representations of the corresponding Lie algebras. With respect to the strong interaction group SU\((3)_\text{colour}\) we need the representations \[\begin{aligned} &\text{singlet} &&\mathbf{1}, \\ &\text{triplet} &&\mathbf{3}, \\ &\text{anti-triplet} &&\mathbf{3^*}. \end{aligned}\] The triplet is the fundamental representation, and the anti-triplet its complex conjugate.

With respect to the weak interaction group SU\((2)\) we need \[\begin{aligned} &\text{singlet} &&\mathbf{1}, \\ &\text{doublet} &&\mathbf{2} . \end{aligned}\] The group SU\((2)\) is pseudo-real so there is no independent \(\mathbf{2^*}\). Finally with respect to the hypercharge group U\((1)_Y\) we will classify fields by their charge as generalisations of electric charge \(q\). The charges turn out to be \[0 \ , \quad \pm \frac{1}{6} \ , \quad \pm \frac{1}{3} \ , \quad \pm \frac{1}{2} \ , \quad \frac{2}{3} \ , \quad \pm 1 \ .\] Moreover the fermions transform as Weyl spinors under the Lorentz group, either left- or right-handed.

Field content

There are the following fields \[\begin{aligned} & \hspace{0.3cm} \begin{pmatrix} \nu_L \\ e_L \end{pmatrix} &&\begin{matrix} \text{neutrino} \\ \text{electron} \end{matrix} &&\text{left-handed} &&\bigg ( \mathbf{1} , \ \mathbf{2} , \ - \frac{1}{2} \bigg ) \\ &\begin{pmatrix} \bar{\nu}_L & \bar{e}_L \end{pmatrix} &&\begin{matrix} \text{anti-neutrino} \\ \text{anti-electron} \end{matrix} &&\text{right-handed} &&\bigg ( \mathbf{1} , \ \mathbf{2} , \ \frac{1}{2} \bigg ) \\ & \hspace{0.6cm} e_R &&\text{electron} &&\text{right-handed} &&\bigg ( \mathbf{1} , \ \mathbf{1} , \ -1 \bigg ) \\ & \hspace{0.6cm} \bar{e}_R &&\text{anti-electron} &&\text{left-handed} &&\bigg ( \mathbf{1} , \ \mathbf{1} , \ 1 \bigg ) \\ & \hspace{0.3cm} \begin{pmatrix} u_L \\ d_L \end{pmatrix} &&\begin{matrix} \text{up-quark} \\ \text{down-quark} \end{matrix} &&\text{left-handed} &&\bigg ( \mathbf{3} , \ \mathbf{2} , \ \frac{1}{6} \bigg ) \\ &\begin{pmatrix} \bar{u}_L & \bar{d}_L \end{pmatrix} &&\begin{matrix} \text{anti-up-quark} \\ \text{anti-down-quark} \end{matrix} &&\text{right-handed} &&\bigg ( \mathbf{3^*} , \ \mathbf{2} , \ - \frac{1}{6} \bigg ) \\ & \hspace{0.6cm} u_R &&\text{up-quark} &&\text{right-handed} &&\bigg ( \mathbf{3} , \ \mathbf{1} , \ \frac{2}{3} \bigg ) \\ & \hspace{0.6cm} \bar{u}_R &&\text{anti-up-quark} &&\text{left-handed} &&\bigg ( \mathbf{3^*} , \ \mathbf{1} , \ - \frac{2}{3} \bigg ) \\ & \hspace{0.6cm} d_R &&\text{down-quark} &&\text{right-handed} &&\bigg ( \mathbf{3} , \ \mathbf{1} , \ - \frac{1}{3} \bigg ) \\ & \hspace{0.6cm} \bar{d}_R &&\text{anti-down-quark} &&\text{left-handed} &&\bigg ( \mathbf{3^*} , \ \mathbf{1} , \ \frac{1}{3} \bigg ) \\ & \hspace{0.6cm} \phi &&\text{Higgs-doublet} &&\text{scalar} &&\bigg ( \mathbf{1} , \ \mathbf{2} , \ \frac{1}{2} \bigg ) \\ \end{aligned}\] where the last expression determines the representations under the gauge symmetries. The fields have several indices corresponding to the different groups, for example \[\big ( u_R \big )^{\dot{a} m}(x),\] where \(\dot{a} \in \{ 1, 2 \}\) is the Lorentz spinor index and \(m \in \{ 1, 2, 3 \}\) is the SU\((3)_\text{colour}\) index.

Three families

The leptons and quarks come in three copies, also known as families. For example, in addition to the electrons and anti-electrons there are also muons and tau leptons with their corresponding anti-particles and an associated neutrino. For the quarks we have discussed this already.

Gauge bosons

In addition to these “matter fields”, there are corresponding gauge bosons, specifically for SU\((3)_\text{color}\) the eight real gluons, for SU\((2)\) three real gauge bosons and one for the abelian U\((1)_Y\) subgroup. After spontaneous symmetry breaking, the SU\((2)\otimes \text{U}(1)_Y\) bosons combine into the two massive complex \(W^\pm\) bosons, the neutral and massive \(Z\) boson and the massless photon. The symmetry breaking itself is due to an expectation value for the scalar Higgs field.

Microscopic action

The microscopic action of the standard model is rather simple. It is a collection of terms we have discussed before. There are kinetic terms for the non-Abelian gauge fields of \(\text{SU}(3)\), of \(\text{SU}(2)\) and the Abelian \(\text{U}(1)\) fields. To do perturbation theory one needs to do gauge fixing, which introduces additional gauge fixing terms and ghost fields.

In addition we have Dirac or actually Weyl kinetic terms for the chiral fermions featureing gauge covariant derivatives for the appropriate representation of \(\text{SU}(3)\), \(\text{SU}(2)\), and \(\text{U}(1)\). This part does not feature any Dirac or Majorana masses, and they are actually not allowed by the symmetries of the model.

For the scalar field in the doublet representation of \(\text{SU}(2)\) there is an appropriate kinetic terms with covariant derivatives, and there is an effective potential with a non-vanishing minimum value featureing spontaneous symmetry breaking.

Finally, there is a set of Yukawa interaction terms coupling fermion and anti-fermion fields, as well as the Higgs-doublet scalar field \(\phi(x)\). When the latter obtains a vacuum expectation value by spontaneous symmetry breaking this also induces Dirac masses for the quarks and leptons, with the exception of the neutrions, which remain massless in the standard model.